Viral Math Problem Sparks Internet Chaos: The Truth About 4 ÷ 2(1)

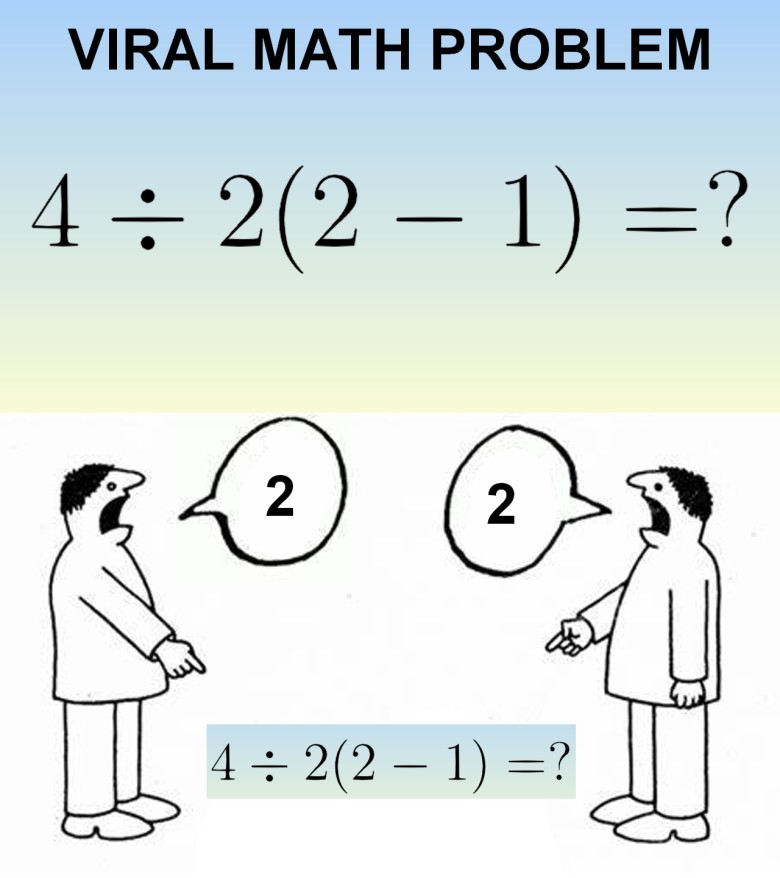
Viral Math Problem: Where Everyone's a Genius Until PEMDAS Enters the Chat

Every so often, the internet rediscovers an old math problem that somehow manages to fracture the collective brain of the digital world. Enter:
4 ÷ 2(1)

If you’ve spent any time online recently, you've probably seen this deceptively simple equation making the rounds again. Some people passionately argue the answer is 1, others insist it’s clearly 8, and chaos ensues. The math forums are ablaze. The meme pages are exploding. And somewhere in the corner, actual mathematicians are just shaking their heads.

The Core of the Debate

Let’s write it out:
4 ÷ 2(1)

Now, depending on how you were taught—or how you interpret the expression—you might see this as:

• (4 ÷ 2) × 1 = 2 × 1 = 2 (Correct according to modern order of operations)

• or 4 ÷ (2 × 1) = 4 ÷ 2 = 2 (Same answer, if you're grouping properly)

But many people incorrectly interpret it as:

• 4 ÷ 2(1) = 4 ÷ 2 × 1 = 2 × 1 = 2 ✅
  Yet, others think it's:

• 4 ÷ 2(1) = 4 ÷ (2 × 1) = 4 ÷ 2 = 2 ✅

However, some mistakenly use:

• 4 ÷ 2(1) = 4 ÷ 2 × 1 = 4 ÷ 2 = 2 → 2(1) = 2 → final = 2

• Or incorrectly say 4 ÷ 2(1) = 4 ÷ 2 = 2 → 2(1) = 2 — which seems fine but can confuse when more complex expressions are involved.

And others bizarrely go:

• 4 ÷ 2(1) = 4 ÷ 2(1) = 4 ÷ 2 = 2, then multiply = 2 × 1 = 2
  ...still right, but only because the extra parentheses don’t really matter unless misread.

So why all the confusion?

Blame It on Ambiguous Notation

The real issue isn't math—it's notation. In professional mathematics, clarity is everything. Mathematicians use parentheses precisely to eliminate ambiguity. This equation is often written sloppily or with implied multiplication (2(1)) that leads people to misinterpret the order of operations.

If it had been written as:

• 4 ÷ [2(1)], then yes, you'd get 1

• If written as (4 ÷ 2)(1), you'd also get 2

But as it stands, PEMDAS (or BODMAS, depending on your country) rules the day:

• Parentheses

• Exponents

• Multiplication and Division (from left to right)

• Addition and Subtraction (also left to right)

So with that in mind:
4 ÷ 2(1) becomes:
4 ÷ 2 × 1
Which equals:
2 × 1 = 2

The Mathematician's Take

Professionals aren’t getting caught in this debate—not because it’s beneath them, but because the question is poorly posed. In academia or technical writing, no one would write 4 ÷ 2(1) and expect perfect clarity. They’d use parentheses to make the operation clear:

• Is it 4 ÷ [2(1)]?

• Or [4 ÷ 2] × 1?

The ambiguity vanishes when better notation is used.

Why the Internet Loves These Fights

It’s a perfect storm:

• Nostalgia for middle school math

• The thrill of being “right” on the internet

• An opportunity to dunk on others with faux confidence

• And a healthy dose of ego

But perhaps most importantly: it reminds us how much we rely on conventions, and how easily they break down in casual use.

Final Thoughts

If the internet has taught us anything, it's that math is a battlefield. But not because it's hard—it’s because clarity in communication matters. Whether you're solving world-changing equations or just battling friends in a comment section, notation and logic win the day.

So next time someone throws 4 ÷ 2(1) your way, take a breath, trust PEMDAS, and remember:

"It's not wrong math—just bad writing."